Boris Steipe
Professor Emeritus
PhD, Ludwig-Maximilians-Universität, Munich, 1990
| Address | Medical Sciences Building, 5316-B 1 King's College Circle Toronto, ON M5S 1A8 |
| Lab | Steipe Lab |
| Office Phone | (416) 946-7741 |
| boris.steipe@utoronto.ca |
Boris Steipe was born in Munich, Germany where he graduated from the medical school of the Ludwig-Maximilians University in 1985. He joined Andreas Plückthun’s lab at the Gene Center of the University for his PhD thesis on the recombinant expression and structure determination of an immunoglobulin fragment. Subsequently, his interests turned to protein engineering, and he joined Robert Huber’s Department at the Max-Planck Institute for Biochemistry in Martinsried, Germany in 1990. It was there that his “Canonical Sequence Approximation” – the hypothesis that sequence propensities can be used to predict stability changes in a very general way was first formulated.
Steipe was appointed Research Fellow at the Gene Center of the University, in 1990 and where his group worked on the rational stabilisation of immunoglobulin domains, on sequence determinants of protein folding and on the interplay of the protein matrix with the fluorophore in Green Fluorescent Protein; he was awarded his Habilitation in Biochemistry at the Faculty for Chemistry and Pharmacy of the University in 2000, when he was appointed as lecturer.
In 2001 Steipe moved to Toronto where he held an appointment as associate professor in the Department for Biochemistry and the Department for Molecular Genetics, University of Toronto. He directed the University’s Specialist Program in Bioinformatics and Computational Biology from 2004 to 2019. He is a Professor emeritus of the Department since July 2022
Research Lab
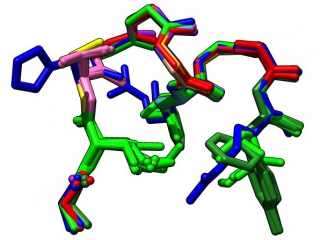
My past work studied sequence/structure relationships in protein structure motifs. My later work focussed on computational systems biology with an emphasis on modelling and data integration. My current work is to develop strategic responses as we navigate the university into the new era of pervasive Artificial Intelligence. To support this challenge, I have founded the Sentient Syllabus Project, and post a newsletter with analysis on the topic.
Learn more: Steipe Lab
Research Description
Computational Biology, Complexity and Society
What ties my research together is the quest to understand complexity in adaptive systems – such as biomolecules, labguage, and society as a whole. Complexity arises from the context dependent behaviour of system components, and in biochemistry we observe it in many hierarchical layers of structure formation, and the generation of function, from the genome to the living cell.
Recent scholarly work (since 2017, with Yi CHEN) has focussed on the question how our understanding of such complex relationships can inform understanding of human relationality – in questions that relate to ethics, as well as aesthetics.
Most recently (2022) I have founded the Sentient Syllabus Project as an international, public-good collaborative to address how academia can re-imagine itself in the face of our new wave of Artificial Intelligence capabilities. This issue sits right at the intersection of my professional expertise and decades of experience in biological- and computer science, the humanities, and education. I publish analyses in the Sentient Syllabus newsletter.
The "Canonical Sequence Approximation"
Theoretical and applied bioinformatics provides core technologies for protein engineering. My lab has contributed two strategies to address the complexity issues that limit rational protein engineering.
The Canonical Sequence Approximation
A first-order approximation is to view amino acids as context-independent elements of protein structure. The hypothesis of a canonical sequence approximation which we have developed, views mutation and selection of the immunoglobulin sequence repertoire in analogy to the concept of an ensemble in statistical thermodynamics. To the degree that mutations are independent and randomly distributed, the most probable distribution of amino acid residues (states) in a canonical immunoglobulin sequence will be described by Boltzmann’s law, where the concept of “energy” is replaced by the “fitness” of a domain in selection. To a large degree, the contribution to fitness will be a free energy contribution to thermodynamic stability of the protein. In the simplest application of this hypothesis, the consensus residues of a domain sequence are predicted to be the most stabilizing residues in their respective positions. This is essentially a mean-field approach, in which amino acid residues are approximated to interact with a context that is averaged over a large number of specific sequences by evolution.
Motif engineering
A second order approximation considers local interactions of amino acid residues only. The concept is the same as above, but this time sequences are aligned from recurring, similar structural fragments from a database of non-related protein structures. We have compiled consensus sequences for these structural motifs and we have been able to show that these sequences can be used for protein engineering.
Non-redundant Subsets for Protein Structure Statistics
Protein Structure Motifs
If a “protein folding code” exists, it ought to give rise to detectable sequence propensities that are associated with low energy conformations, i.e. native structure. To the degree that the frequency of structure patterns in folded proteins has a Boltzmann-like behaviour, such conformations should be detectable by their excess occurrence over random. We have mined a database of non-homologous, well resolved protein structure domains – Nh3D – and have discovered an abundance of such sets of overrepresented structurally similar patterns. We designate the best representatives of a set a motif. Our motif dictionary schematikon shows significant and interesting sequence propensities and is predictive regarding the experimentally determined consequences of sequence change on stability.
Courses Taught
BCH441H (BCH1441H) Bioinformatics
BCH2024H Biological Data Analysis with R
Extra-Departmental Courses
MGY441 Bioinformatics
CSB195 Foundations of Computational Biology
Publications
View all publications on PubMed
schematikon: Detailed Sequence-Structure Relationships from Mining a Non-redundant Protein Structure Database
Boris Steipe and Bhooma Thiruv
Bioinformatics Research And Applications - Springer Lecture Notes in Computer Science Volume 8492, 2014, pp 357-366 Read
Nh3D: a reference dataset of non-homologous protein structures
Bhooma Thiruv, Gerald Quon, S. Adrian Saldanha and Boris Steipe
BMC Struct Biol. 2005 Jul 12;5:12. Read
Consensus-based engineering of protein stability: from intrabodies to thermostable enzymes.
Boris Steipe
Methods Enzymol. 2004;388:176-86. Read





